Spastic Gasket
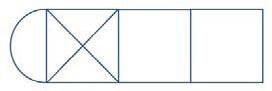
A robotic applicator needs to extrude a gasket in the above shape without stopping the flow of the gasket mate- rial – or retracing any of the lines. The robotic arm can start and end the extrusion at any position along the path. Can you find the path that will allow a continuous extrusion for the gasket?
Circular Reasoning

An eccentric factory owner has a large circular conveyor measur- ing 27 feet in circumference in the center of his factory. She wishes to place 6 sensors in positions around the conveyor such that one sen- sor or another is at a distance of one, two, three… up to twenty six feet from some other sensor. In other words, she wishes that all the integer value distances from one to twenty-six feet will be measurable between some pair of the sensors. Where should she place the sensors?
Extra Credit: How much longer could the circular conveyor be, and still allow placement of the 6 sensors with all the integer distances represented (up to the new-circumference-distance less one foot)?
Goofy Golf
A certain nine-hole golf course has the following yardages for each hole: 300, 250, 200, 325, 275, 350, 225, 375, & 400. If a golfer could hit one of exactly two distances on every stroke, so that the ball would go directly toward the hole, pass directly over the hole, or go in the hole – what two distances would be optimal for play- ing the course with the fewest number if strokes? For example, the two distances of 125 yards and 75 yards would get a golfer around the course with 28 strokes – but this is not the lowest score possible?
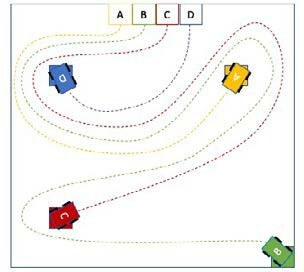
ABCs for AGV

The puzzle factory’s four Automated Guided Vehicles (AGVs) all leave their charging stations one morning for their first pickups. A is to pick-up at location A, B at B, and so on. But the owner of the fac- tory has stipulated that none of the AGVs should cross the path of any other, on this first trip. Can you find a path for each AGV that will get it to its destination, without crossing the paths of the other AGVs (or leaving the confines of the factory: the outer border)?
Scroll Down for Solutions
–
–
–
–
–
–
–
–
–
–
Brain Teaser Solutions
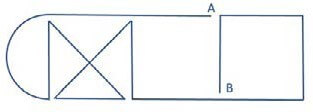
Spastic Gasket –
The applicator can start at point A or B to trace the following (approximated) path in either direction.
The Circular Conveyor-
Place one sensor at any point on the conveyor (call that position zero), then place additional sen- sors at 1, 5, 9, & 12 feet respectively from position zero. The remaining gap from the last sensor back to the first sensor (completing the circle) should be 14 feet. Extra credit: the conveyor can be increased in length to 31feet,andsensorsplacedatthe0,1,3,8,12,&18footmarks. The general solution: for a sensor count of n sensors, the formula n(n-1) will define the num- ber of integer distances possible (with n = 1, 2, 3, 4, 5, 6). So, for 6 sensors, all the integer distances from 1 to 30 are possible on a 31 foot conveyor. [Extra credit reference Michael Goldberg’s solution to Problem E1716 in American Mathematical Monthly, September 1965, p. 786.}
Goofy Golf–
The two distances of 100 yds and 125 yds will yield a low score of 26 strokes. Let’s call the 125 yard stroke the ‘drive’, and the 100 yard stroke the ‘approach’. The first hole is 300 yards, so the golfer uses three approach shots. The second hole simply needs two ‘drives’. The third hole; two‘approaches’. The fourth at 325 requires one drive and two approach shots. The fifth is per- haps the trickiest of all; the golfer overshoots the hole with three drives, and then uses one approach shot to get back to the hole The sixth at 350 uses two drives and one approach. Hole seven is one of each dis- tance. The eighth is three approaches, and the ninth is four drives. Thus resulting in a score of 26 strokes.
ABC’s for AGV’s –