In each issue of the Automation Notebook we feature a section of brainteasers. These are the brainteaser answers from Issue 16, 2010 of the Automation Notebook. The brainteaser questions are repeated in black. The answers to the brainteaser questions are highlighted in red with explanations. You can view the brainteasers from Issue 16, 2010 without the answers here: http://library.automationdirect.com/brainteasers-issue-16-2010/
1. Is bigger really better?
Let’s say your goal is to reduce gasoline consumption.
And, let’s say there are only two kinds of cars in the world. Half of them are Suburbans that get 10 miles to the gallon and half are Priuses that get 50.
If we assume that all the cars drive the same number of miles, which would be a better investment:
• Get new tires for all the Suburbans and increase their mileage a bit to 12 miles per gallon.
• Replace all the Priuses and rewire them to get 100 miles per gallon (doubling their average!)
Extra Credit: How fuel efficient would the Priuses have to be in order to best the 2 mpg increase in the Suburbans?
Credit: Seth Godin
Answer:
Believe it or not, the new tires for the Suburbans would be the most effective strategy for reducing gasoline consumption. The average fuel economy of the original fleet is 16.6 MPG. A 2 MPG increase for the Suburbans raises the fleet’s economy to 19.4 MPG. Doubling the Prius’ millage only increases the fleet’s MPG to 18.2. The Surburbans are burning 80% of the gas, so a small change for them has more effect.
Extra Credit:
In order for the Prius’ mileage to have a greater effect than the 2 MPG increase for the Surburbans, the Priuses would have to get more than 300 MPG.
Fleet fuel economy is calculated using a harmonic mean. For example, a fleet of 4 vehicles getting 15, 13, 17, and 100 mpg has an average fuel economy of slightly less than 19 mpg:
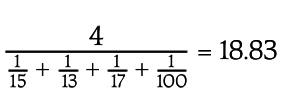
2. Crosscut
Can you cut a symmetrical “Greek” cross (shown) into five pieces, so that one piece will be a smaller symmetrical Greek cross, and the other four pieces will
fit together to form a perfect square?
Answer:
3. Crossways
Can you arrange these four pieces (cut from a square as shown) to form a symmetrical Greek Cross?
Answer: