In each issue of the Automation Notebook we feature a section of brainteasers. These are the brainteaser answers from Issue 23, 2012 of the Automation Notebook. The brainteaser questions are repeated in black. The answers to the brainteaser questions are highlighted in red with explanations. You can view the brainteasers from Issue 23, 2012 without the answers here: http://library.automationdirect.com/brainteasers-issue-23-2012/
1. The Curly Shuffle
A factory has three CNC machines – each with its own operator. One day a large order is received and Larry quickly boasts “Curly and I can produce all those parts in ten days, but if you let Moe help me instead of Curly, we can do it in 9 days”. Curly is offended, and replies “Forget about Larry, if Moe and I produce the parts, we can finish in 8 days”. How long would it take each CNC operator to produce all the parts on his machine individually?
Answer:
Larry: 23 7/31 days
Curly: 17 23/41 days
Moe: 14 34/49 days
2. Cable Tie-up I
Can you remove four cable ties from the following arrangement and leave four equal size triangles with no extra “offshoots” or loose ends?
Answer:

3. Widgetry
During the morning shift the probability of a widget passing by a certain sensor (on a conveyor belt) in a 20 minute window is 0.9. What is the probability of a widget passing that sensor in a 4 minute window? Please assume a constant probability throughout the shift.
Answer:
Probability of a widget passing in a 20 minute window = 1 – (probability of no widget passing in a 20 minute window)
Probability of a widget passing in a 20 minute window = 1 – (1 – probability of a widget passing in a 4 minute window)^5
0.9 = 1 – (1 – x)^5
(1 – x)^5 = 0.1
1 – x = 10^(-0.2)
x = 1 – 10^(-0.2) = 0.369
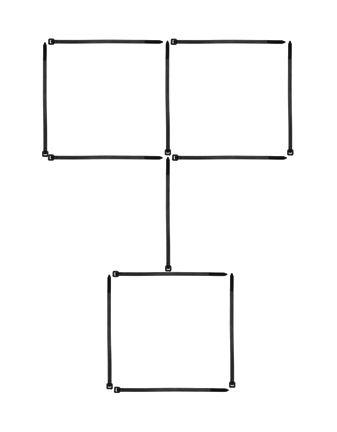
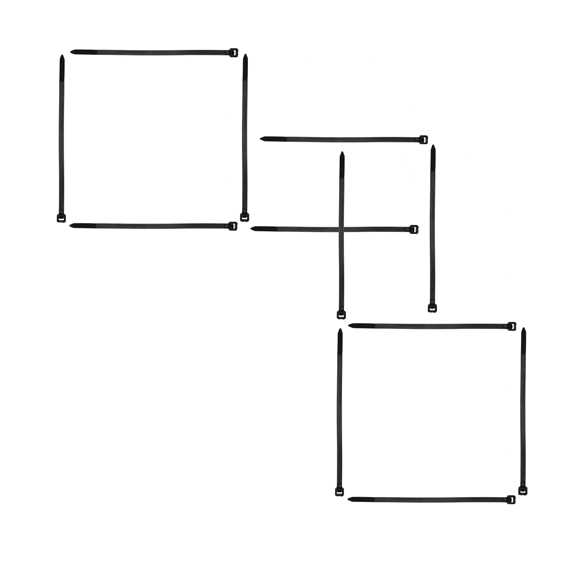
4. Cable Tie-up II
Starting with the arrangement shown above can you move only six of those cable ties and produce a pattern with five (unique) squares? No doubling-up the cable ties or loose ends, please.
Answer:


1 Comment