In each issue of the Automation Notebook we feature a section of brainteasers. These are the brainteaser answers from Issue 27, 2013 of the Automation Notebook. The brainteaser questions are repeated the answers are posted below each question. You can view the brainteasers from Issue 27, 2013 without the answers here: http://library.automationdirect.com/brainteasers-issue-27-2013
The ‘bot is in Your Court
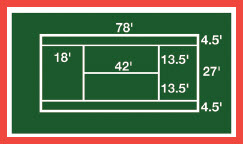
The local robotics team has come up with a robot designed to automatically paint the lines on a standard tennis court. The only issue with the robot is that turning the paint on and off makes a mess, but the team has realized that going over a line twice will work just fine. They don’t want to waste any more paint than is absolutely necessary, so their challenge is to find a starting point and a route that will paint all the lines at least once, while minimizing the overall trip length. What would be the route (shortest distance) that the robot could take to paint the lines?
Solution:
There are a number of ways to paint the lines on the court (without turning the paint on and off) by adding only 63’ of length to the total path. One solution is shown below. The robot needs to travel the long solid path once and adding the dotted line portions (as out-and-back trips) when it passes by either end of those portions. This solution can be flipped and/or mirrored, but the basic premise remains the same. The total length of all the stripes is 480 feet, but with the 63 feet of retracing, the total route length the robot must travel is 543 feet.
Answer: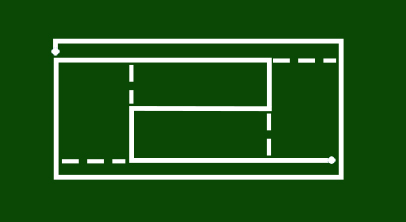
To solve this problem logically, consider the number of “odd vertices” – that is, vertices from which you can go in three directions. In this mesh, there are 10 of those. This tells us that we can connect all of those nodes with 5 unique paths (10÷2). Then look for the four shortest paths between such vertices that do not share a vertex, those four are the ones that will have to be retraced while we traverse the fifth (longest) path. Those four short paths can be either two of the (non-connected) 13.5 foot segments and the appropriate two 18 foot segments that do not connect directly to the chosen 13.5 foot paths. Once you have chosen the four short segments, it’s fairly easy to trace the fifth and longest path. To finalize the solution, follow the long path, starting and ending anywhere along its length, and pick-up each of the four short paths (as out-and-back “side trips”) when you reach either of its endpoints.
That Rhino Sure is Zippy
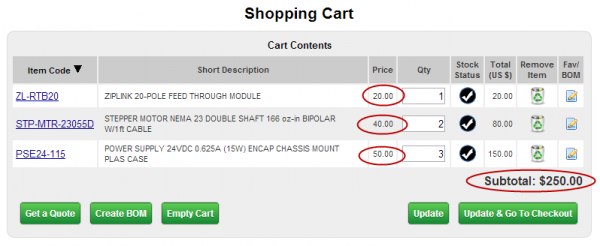
Otto went shopping at AutomationDirect.com for some supplies for his factory. He bought one Ziplink™ Module, two SureStep™ Stepping Motors, and three Rhino Encapsulated Power Supplies. He spent a total of $250 exactly (and he even got free shipping). But he lost his paperwork and forgot the prices of the three items (he also forgot that he could review all his purchase history, and even reprint past invoices on the Web store). All he could remember was that the price of three of the ZipLink modules plus one of the SureStep motors totaled exactly the same as the price of two of the Rhino Power Supplies. Can you help him figure out the actual prices of the three components?
Answer: ZipLink – $20, SureStep – $40, Rhino – $50
And thanks and congratulations to George Miller for alerting us to another valid answer to this brainteaser. He found that ZipLink – $41, SureStep – $7 and Rhino – $65 would also work.
Any others? Drop us a line editor@automationnotebook.com if you can find another solution.
Production Deduction
The shiny new automated machine in the puzzle factory produced one-fourth of the day’s total production of puzzles before the morning break, then it produced one-fifth between the morning break and lunch. Another one-third of the total was produced between lunch and the afternoon break. After the afternoon break it produced 13 puzzles. What was the overall production total for the machine that day?
Answer:
Solve for x:
x = (x/4) + (x/5) + (x/3) + 13
x = 60
Overall Production Total = 60 Puzzles
Cable Tie-up
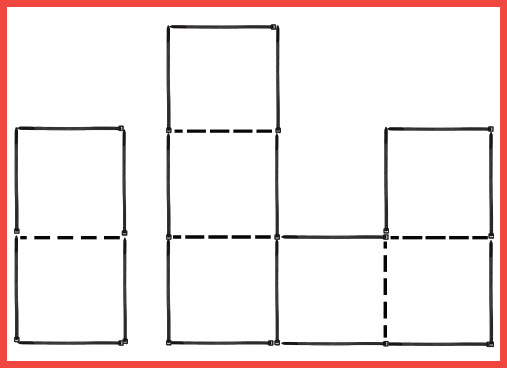
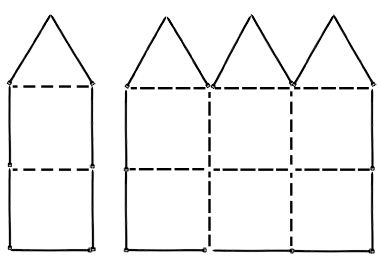
With the cable tie layout shown, you might notice that the larger shape encloses exactly three times the area of the smaller. Can you move one cable tie from the larger group to the smaller, and still have the larger shape enclose exactly three times the area of the smaller? Remember, 12 of the cable ties must remain in their current positions, and no doubling-up the cable ties or loose ends, please. The dotted lines are shown only to help visualize the areas of the two shapes.
Answer:
Did you know that AutomationDirect sells high-quality cable ties at the lowest prices on the web? Visit: www.AutomationDirect.com/cable-ties for more information and to see our great prices!