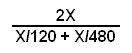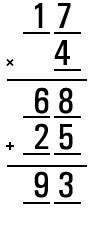In each issue of the Automation Notebook we feature a section of brainteasers. These are the brainteaser answers from Issue 3, 2005 of the Automation Notebook. The brainteaser questions are repeated in black. The answers to the brainteaser questions are highlighted in red with explanations. You can view the brainteasers from Issue 3, 2005 without the answers here: http://library.automationdirect.com/brainteasers-issue-3-2005/
1. “Next Day Air”
An AutomationDirect purchasing agent flies from our Cumming, GA facility to visit one of our vendors on the most economical flight she can find (two stops, one plane change). The average speed of the outbound trip (including the stops) is 120 mph. For the return trip, a jet is chartered to deliver all of the urgently needed products to our warehouse as fast as possible. It averages 480 mph on the return trip.What is the average speed for the entire trip?
Hint – It’s not 300 MPH!
Answer: To determine the average speed for the entire trip, we need to find a way to represent the total Miles and divide by the total Hours. We do not actually need to determine either value. Assume the trip was a distance of ‘X’ miles. The outbound trip therefore took X ÷ 120 hours. The return trip; X ÷ 480 hours. The total miles then are 2X, and the total trip time is (X ÷ 120) + (X ÷ 480) hours.
If we express this in Miles per Hour, we have:
Or, more simply: 2X (480) ÷ 5X MPH
The X’s divide out, resulting in an average speed for the entire trip of: 192 MPH.
2. Fill-in-the-blanks
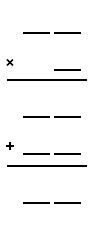
Use each of the numbers 1 – 9 to fill-in the blanks and complete a valid pair of equations:
Answer:
AutomationDirect would like to credit an 1800th century mathematician – Henry Ernest Dudeney (10 April 1857 – 24 April 1930) for this brainteaser.
3. “Think outside the blocks”
Fred wants to use a pair of wooden blocks (cubes) to display the day-of-the-month on a simple desk calendar. How can he number two blocks (one number per side) so that he can display all the dates of any month: 01 – 31?

Bonus puzzle: Ignoring the many solutions made possible by re-arranging a given set of numbers on a block, how many ways can he assign the numbers to the two blocks?
Double bonus: What is the total number of ways to number the blocks including the re-arrangement possibilities?
Answer: With 2 six-sided blocks to work with, we have 12 total sides to place numbers on. In order to display all of the dates from 01 to 31, we need to assign the ten numbers 0 – 9, and we need some extra numbers. A ‘0’, a ‘1’, and a ‘2’ need to be present on both blocks to form all the required combinations. This is seemingly a total of 13 numbers that need to be assigned to the 12 sides of the blocks. The ‘trick’ is to realize that a single side of one block can display ‘6’ and‘9’ by simply turning the block over. It is then a fairly simple matter to arrange the numbers. One solution would be: 0, 1, 2, 3, 4, 5 on the first block and 0, 1, 2, 7, 8, 9 (or 6) on the second.
Bonus puzzle: with the first three numbers (0, 1, and 2) required on both blocks the unique combinations for assigning 3 of the remaining 6 numbers to each block is 20 . This puzzle involves the use of the mathematical concept of “combinations”. The answer is a “binomial coefficient”, sometimes referred to with the expression “6 choose 3” (which is written 6_C_3). The answer can be calculated using “factorials” as in (6!) / (6-3)! × 3! That’s 720 ÷ 36 = 20. Pascal’s Triangle can also be used to find the answer.
Double Bonus: The total number of ways that the numbers can be arranged is found using “Permutations”. A given set of 6 numbers can be assigned to one block 6! (read ‘six factorial’) ways, or 720 different ways. If there are 20 unique ways to assign the numbers to the blocks, and 720 ways to arrange the numbers on each block, then the total number of possibilities would be 720 × 720 × 20 = 10,368,000. More information about Permutations and Combinations is availablehere .