1.) Loopy Lapel
To setup this puzzle: drill a hole in a pencil and tie a loop of string through the hole (as shown in the picture). Make sure that the loop of string is short enough that it will NOT pass over the long end of the pencil (the pointy end). 
Now, the trick: without untying the string, or sharpening/shortening the pencil – can you loop the pencil/string assembly through a button hole? Like this: 
It’s a neat trick to play on an unsuspecting friend – after you have discovered the secret, and have practiced it a few times…
Ask the friend to look away for a second and slip it into a button hole on their blazer. Then watch them scratch their head while trying to remove it 😉
2) Algebradabra
Find all real numbers x such that:
![]()
3) Alphametics
Each letter in an “alphametic” represents a single numeric digit. Each letter represents the same digit each time it occurs, and two different letters never represent the same digit.
The most famous of these is probably: 
The story goes that this was the text for the least expensive telegram that a destitute traveler could send back home – and it includes both the request for help AND provides the amount of MONEY needed. If you are too young to remember: telegrams were charged per character transmitted. (Maybe we should return to that model to cut down on spam!)
And if you haven’t seen that one before – give it a try – it’s a great puzzle.
But here is an interesting pair of alphametics for which a single solution will solve both: 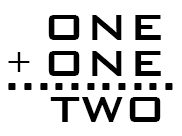
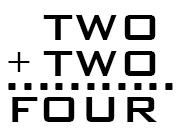
But here’s the rub: a solution that holds for both equations is not possible with our standard “base 10” number system.
Can you determine the solution and the smallest positive integral base for that solution?
[Credit: Mathematics Student Journal – circa 1965]

