Application Complication
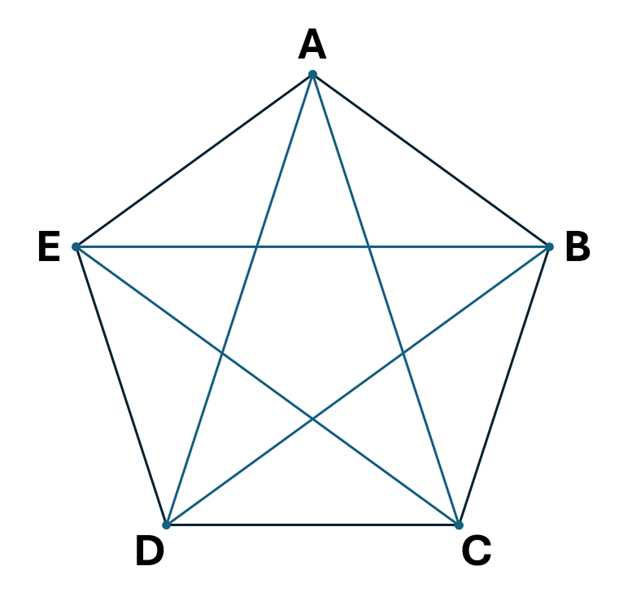
The programmer for the gasket applicator robot at the puzzle factory noticed that there were a number of different tool paths that could be used to program the gasket path required for a new mechanical puzzle. The complete pattern is shown below. He must apply the gasket in a continuous bead along all the lines shown, but he can only change direction at the outer points (labeled A-E) with no interior turns. And all tool paths must begin (and end) at the point labeled A. How many possible paths are there?
The Style
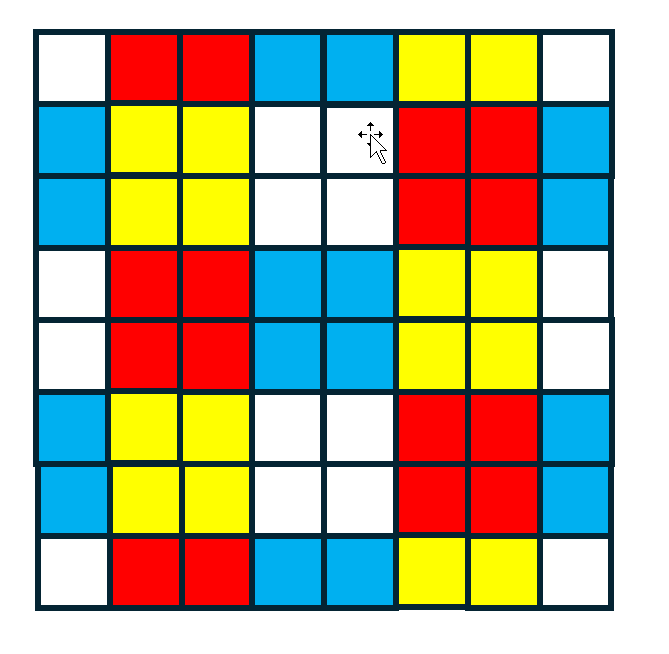
Can you arrange any 16 of the following tiles into a square such that like colors (of all the tiles) are touching on all sides? You can choose any of the 16, and you may rotate the tiles as needed.

Coupling Shuffling
The puzzle factory engineer has labeled 10 couplings with numbers from 0 -9 and arranged the couplings in a pyramid such that the totals of the numbers on each side of the pyramid add up to 16. What is the smallest sum (on all sides) that can be achieved by rearranging the couplings? You might note that the coupling in the center is not used in any of the sums.
Did you know… that Automation Direct sells a wide range of shaft couplings, and bore reducers? With coupling styles such as jaw (hub and spider), Oldham, double loop, servo beam, and servo high gain varieties, we have the coupling you need for reliable power transmission (with little or no backlash) and to compensate for shaft misalignment. https://go2adc.com/couplings

Answers Below
.
.
.
.
.
.
.
.
.
.
.
Application Complication
There are 264 possible routes.
The Style
Discard the first tile in each horizontal row and arrange the remaining tiles as shown below.
Coupling Shuffling
There are 16 discrete solutions all resulting is a sum of 13 on each side. All the solutions are variations of the following two examples (the inner two couplings on each side can be swapped independently, or in combination). It’s no accident that the highest number is placed in the center, where it is unused in any sums, AND that the lowest values are placed in the corners.


