Tie Fighter
Let’s number the 4 ties that we plan to move:
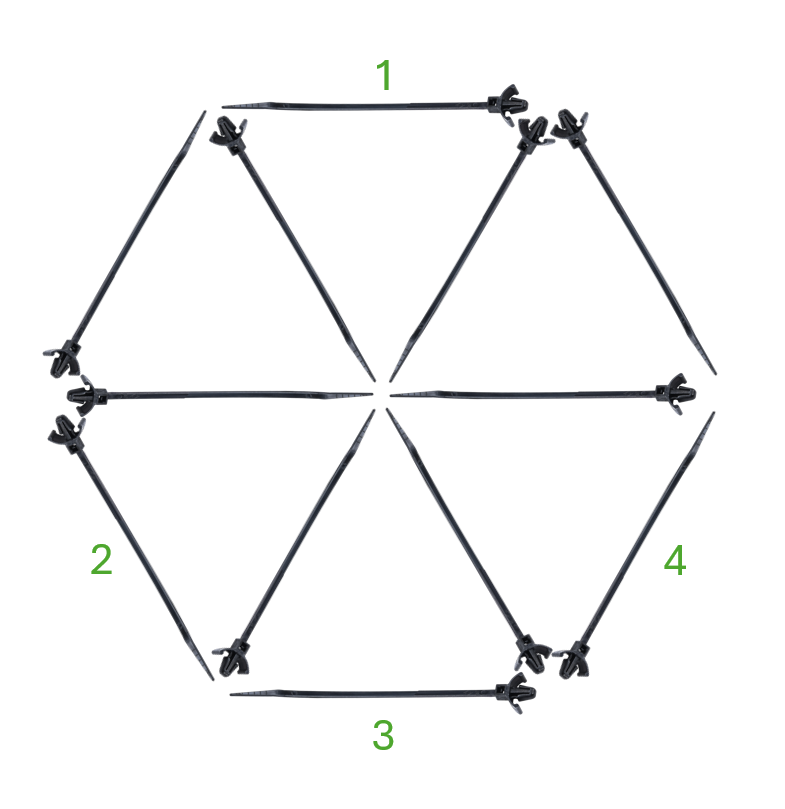
Then move them to these new positions:
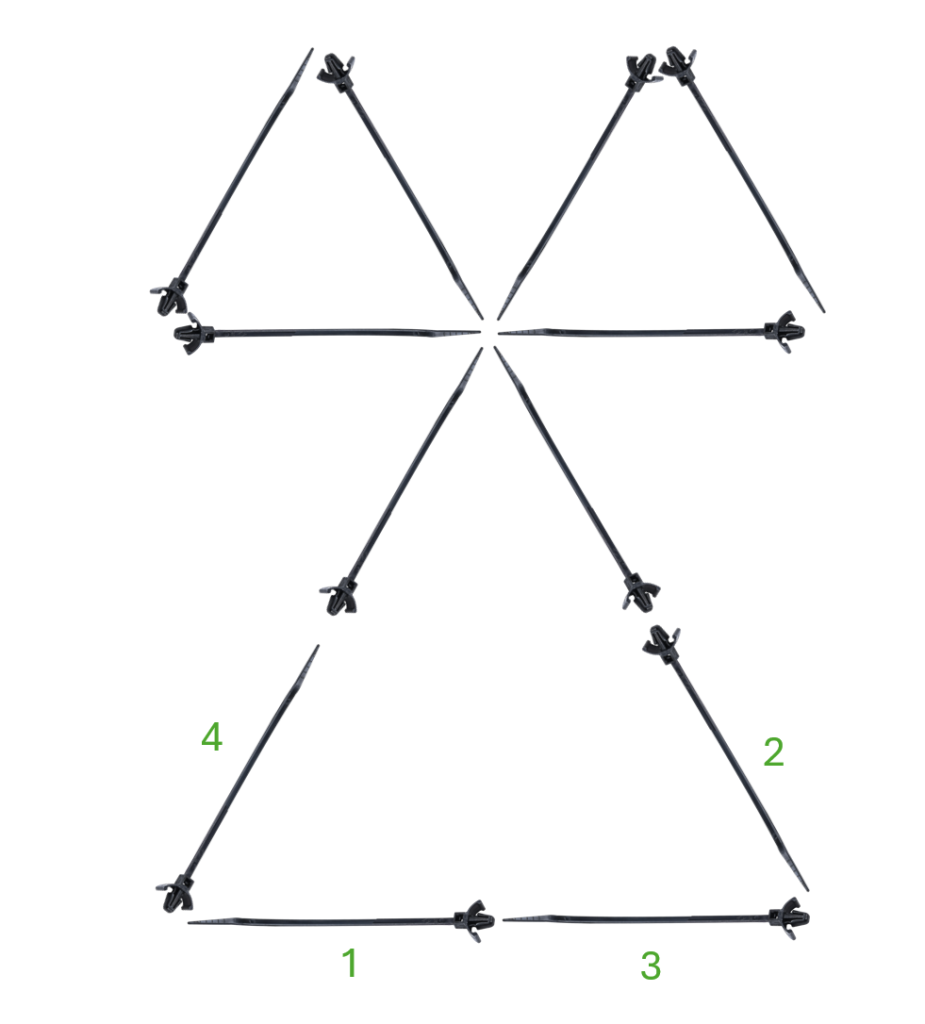
Do Your Level Best
Here is a sketch of the tank with the block lowered into place. Let h represent the height of the increased level (as shown) that we wish to determine.
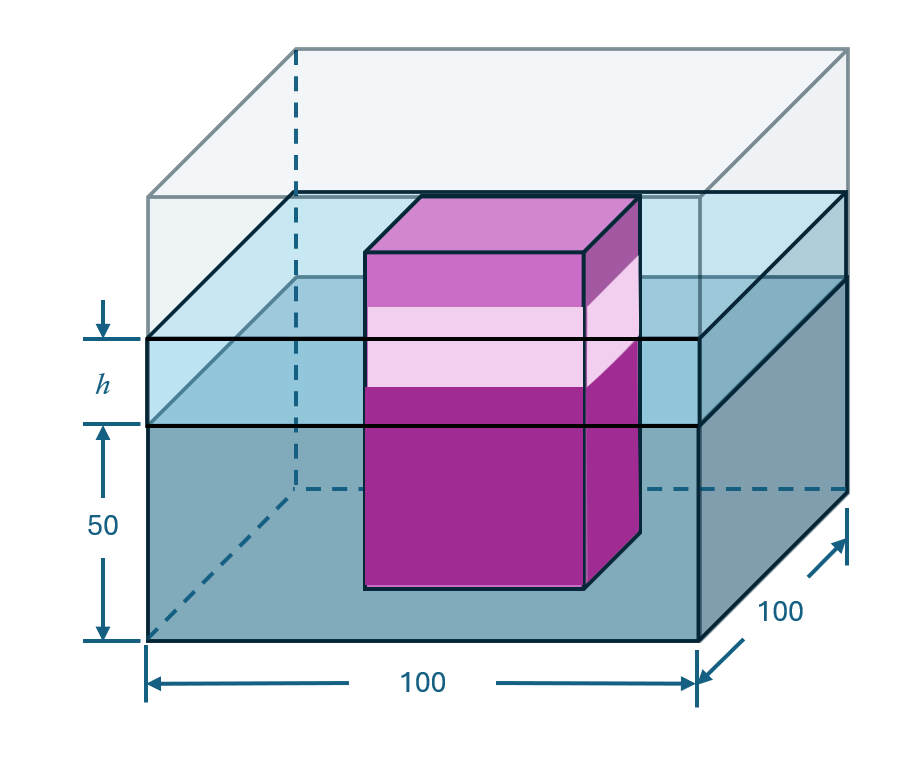
Let’s also label three areas:
D = the area of Displaced liquid (lower section shown in dark purple) = 50 x 50 x 50
I = the area of the Increased liquid level (section shown in light blue) = 100 x 100 x h
B = the area of the Block section that is inside the increased liquid level (shown in light purple) = 50 x 50 x h
It should follow that D = I – B
50 x 50 x 50 = (100 x 100 x h ) – (50 x 50 x h)
150,000 = 1002h-502h
150,000 = (1002-502)h
150,000/7,500=h
h =20
So, the liquid level will rise by 20 units once the block is lowered into the tank.
Triple Tangency
There are several ways to solve this problem – but this one seems a little easier than most.
Let’s call the radius of the circle r, and add some other known measurements; the Two Tangent Theorem states that the two distances from any external point (such as A or B) to two points of tangency on a circle are always equal. It may help to draw the shared hypotenuses (of right triangles) from either A or B to the center of the circle, to help visualize the reasoning behind the Two Tangent Theorem.
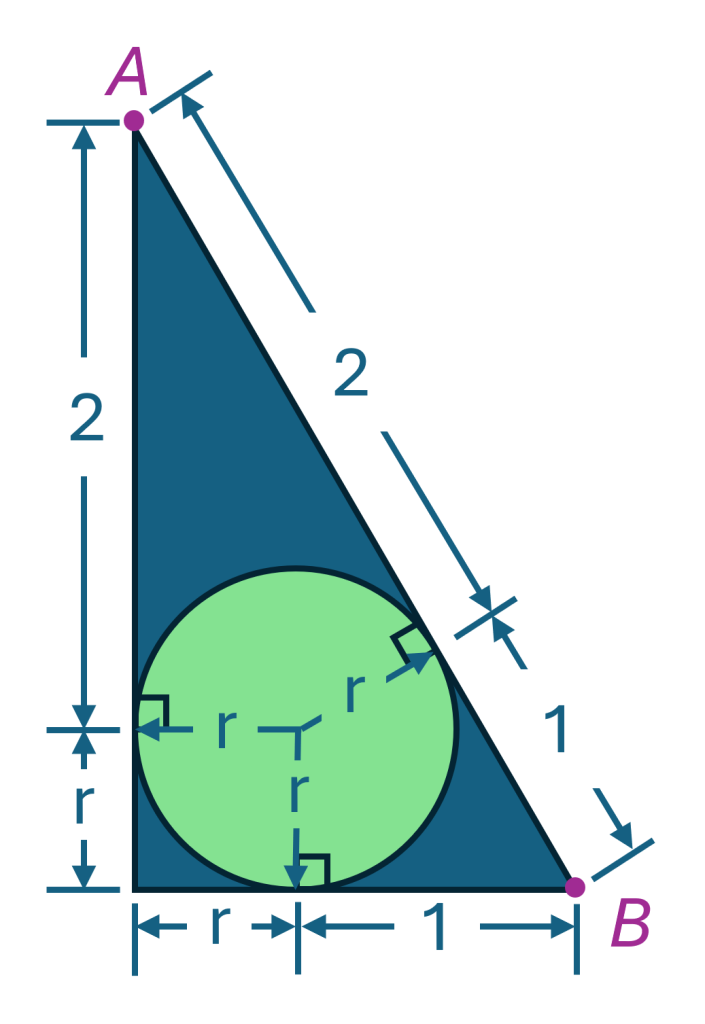
Because this is a right triangle, we know that the sum of the squares of the sides is equal to the square of the hypotenuse. So:
(r + 1)2 + (r + 2)2 = 32
2r2 + 6r + 5 = 9
r2 + 3r – 2 = 0
While we could solve for r, we really aren’t looking for r. And this little trick (adding 4 to both sides) saves us some work:
r2 + 3r – 2 + 4 = 4
r2 + 3r + 2 = 4
And the area of a right triangle is height times base divided by two:
Area = (r + 1)(r + 2)/2
= (r2 + 3r + 2)/2
And from the first equation we know that r2 + 3r + 2 = 4, so:
Area = 4/2
Area = 2

