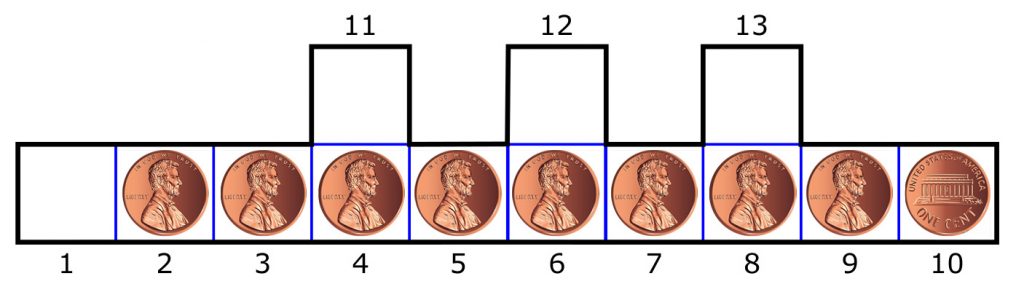
Changing a Penny
Given the diagram below, what is the minimum number of “moves” to get the obverse penny (in square 10) to the far left end of the row (square 1). The pennies may NOT be lifted from the page, nor can they leave the bold-bounded area. When counting each “move” a penny can move any distance possible (subject to those two constraints) in a single move.
eSlicer
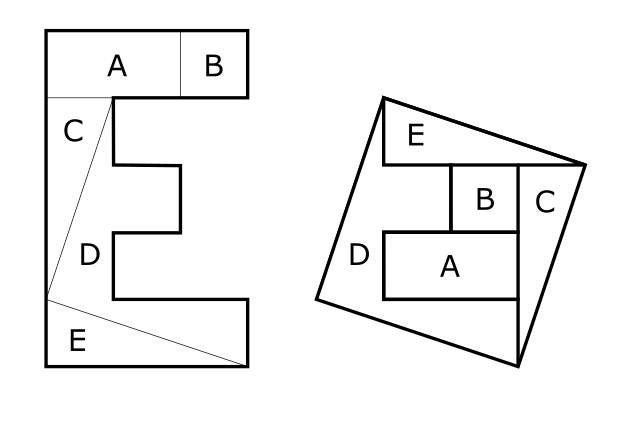
Can you cut the “E” into five shapes that will reassemble into a perfect square? No flipping of the cut parts. The dimensions are shown for clarity.
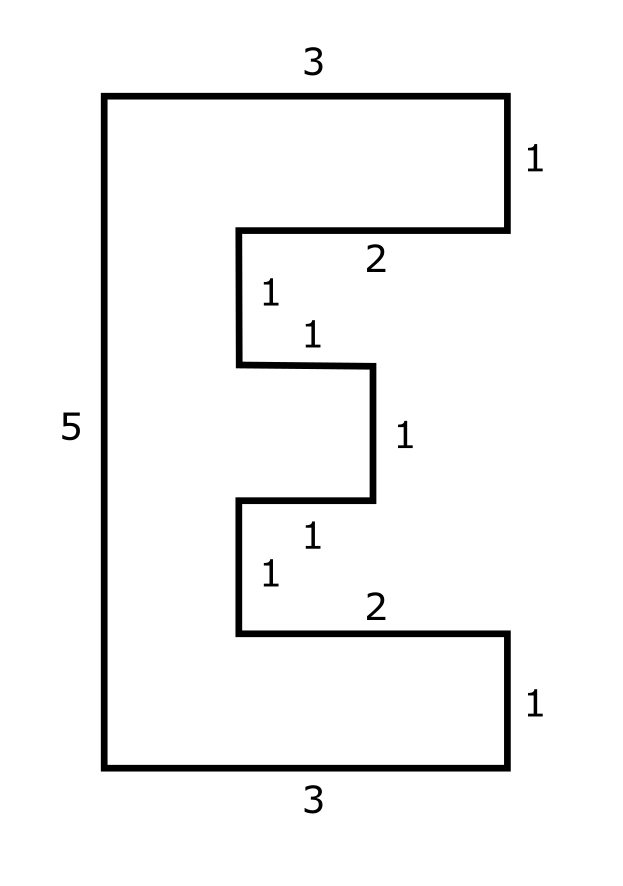
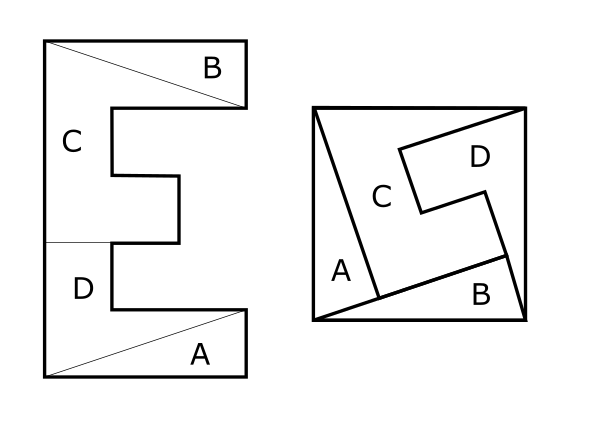
Extra Credit – if you are allowed to flip the cut pieces, can you do it with just four pieces?
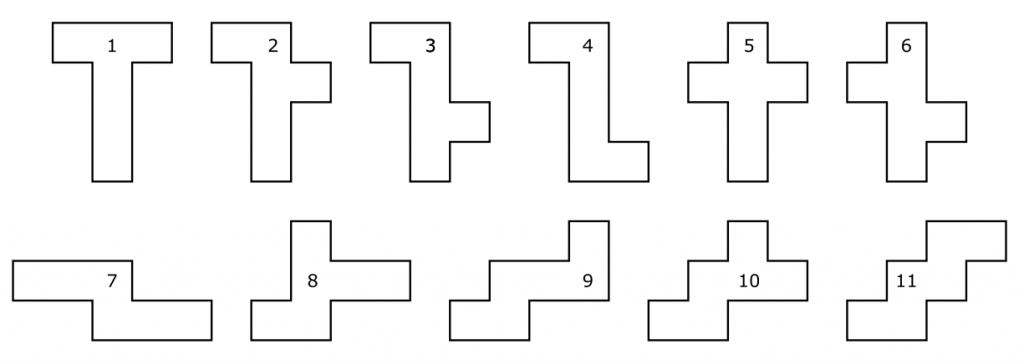
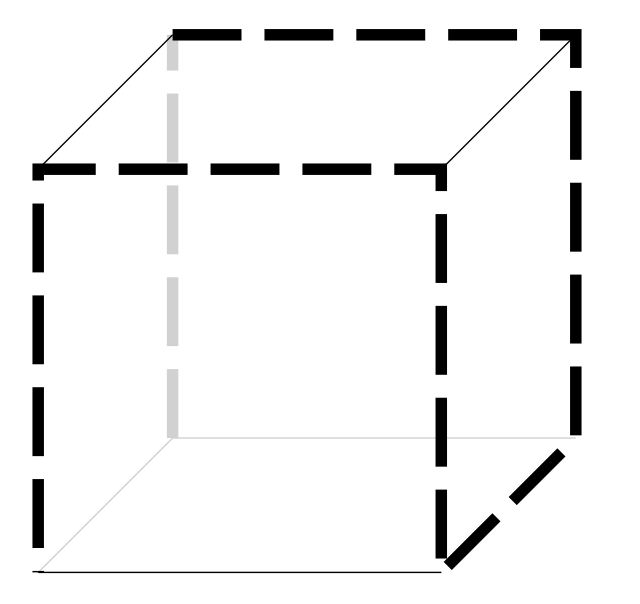
Unfolding a Cube

Start with a regular cubic box – and slice along 7 contiguous edges to allow the box to unfold to a flat shape. Discounting any shapes that are mirror images of each other, how many different shapes are possible?
For example – if you cut along the dashed lines shown in the following example and unfold – then a “T” shape will result.

All puzzles credited to: Henry Ernest Dudeney (1857 – 1930)
Answers Below!
.
.
.
.
.
.
.
.
.
.
Answers
Changing a Penny
Let’s number the pennies as shown in this updated diagram:
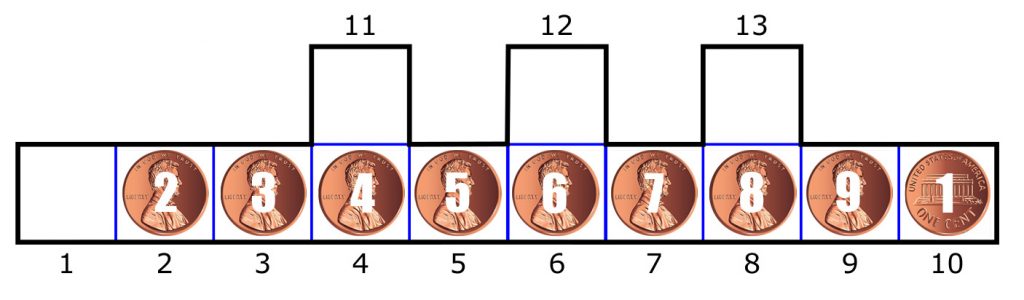
Here are the 20 moves (the first number is the penny – the second number: the number of the square where it ends-up):
- (2:1) (3:2) (4:3) (5:11) (6:4) (7:5) (8:12) (9:6) (1:13)
- (9:10) (8:9) (1:12)
- (7:13) (6:8) (5:7) (1:11)
- (4:12) (3:6) (2:5) (1:1)
ESlicer
Five pieces, no flipping:
Extra Credit – Four pieces, with “D” flipped:
Unfolding a Cube
A total of 11 shapes are possible (without the mirrored versions). If you count the mirrored versions there are 20 total. Shapes 1 and 5 are identical if mirrored.