Brainteasers, Issue 55, 2025

Polka Dot Remainder

Find the area of the blue shaded portion in each figure below:

Area Sensors

Answers Below

.

.

.

.

.

.

.

.

Polka Dot Remainder

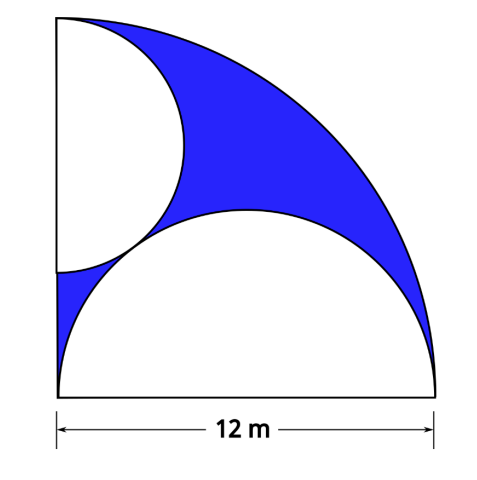
It’s obvious by inspection that the area of the blue shaded portion is equal to the area of the big quarter circle minus the areas of the two smaller half circles.  The area of the big quarter and lower half are easy to calculate. But we need to know the radius of the upper half circle, in order to calculate its area.

Note the right triangle described below:

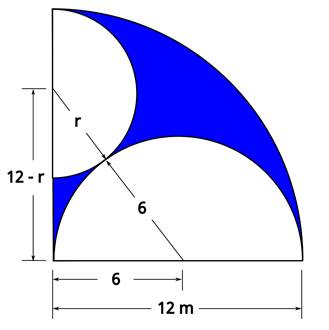
Start by finding r. Where r is the radius of the smaller half circle.

Using the Pythagorean theorem (square of the hypotenuse of a right triangle is equal to the sum of the squares of the sides):

(6 + r) ² = 6² + (12 – r)²

36 + 12r + r² = 36 + 144 – 24r + r²

36r = 144

r = 4

Now we can calculate the areas of the three circle sections

Area of the big quarter circle: 1/4π12² = (144/4)π = 36π

Area of the lower half circle: 1/2π6² = 18π

Area of the upper half circle:  1/2π4² = 8π

And thus: the area of blue shaded portion is the area of the big quarter circle less the areas of the two smaller half circles: 36π – 18π – 8π = 10π  (or approximately 31.4)

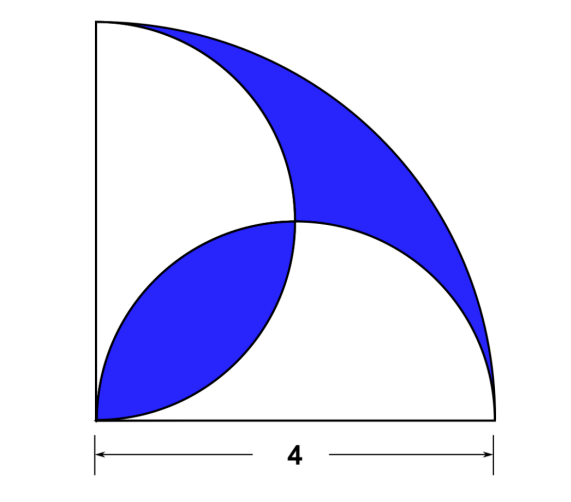
Under My Umbrella

To start the solution let’s superimpose a 2 x 2 grid over the lower part of the figure:

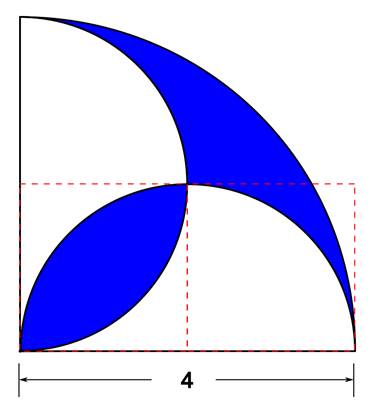
Then let’s color the two areas below – for clarity:

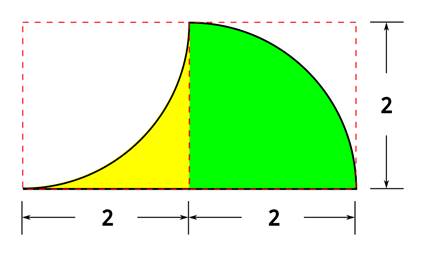
If we can determine the areas of the yellow and green portions of the figure, we can subtract that total area x 2 from the area of the larger quarter circle – and determine the answer.

The yellow shaded portion has an area of 2² – 1/4π2²   =   4 – π

The green shaded portion has an area of 1/4π2²  =  π

So, the combined area for the yellow and green areas is:  4 – π + π   =  4

(note that you could rotate the yellow section to fit above the green and complete a 2×2 square.  Also with area = 4)

The large quarter circle has an area of 1/4π4² = 4π

Therefore, the area of the entire blue shaded portion is 4π – 8  (or approximately 4.566)

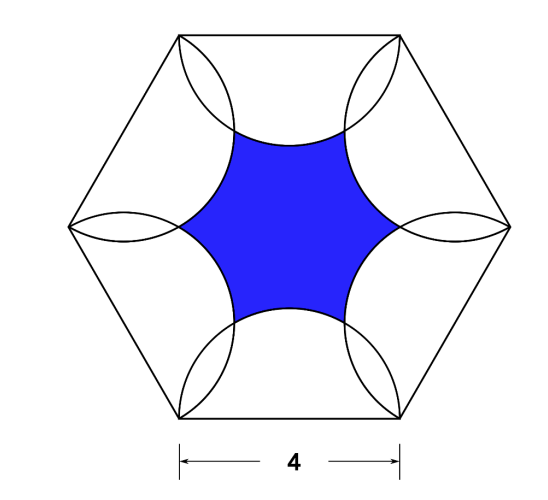
Hexagonal Detangle

Let’s start by superimposing a grid of equilateral triangles with 2” sides

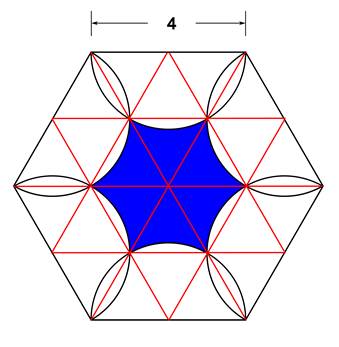
Then focus on a pair of the triangles at the bottom center of the figure:

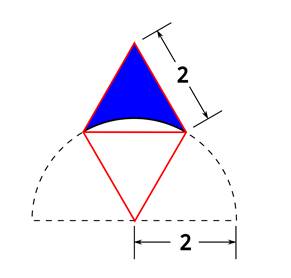
From this figure, it’s possible to subtract 1/6 the area of a 2” radius circle from the area of two of the equilateral triangles to determine the area of 1/6^th of the total blue area.

• The area of one of the triangles can be found using the formula for equilateral triangles A=(√3/4)a²

(where ‘A’ is area, and ‘a’ is the length of one side).  A = (√3/4)2² = √3

• You could also find that area using the Pythagorean theorem. The height of the triangle is 2² – 1² = h² so, h=√3.  And the area is height x ½ base-length, or √3 x 2/2 = √3

• So, the area of two of the triangles is 2√3

• The area of 1/6^th of a 2” radius circle is (π2²)/6 = 2π/3

So, 1/6^th of the blue shaded area is 2√3 – 2π/3 (this is the area of the blue portion of a single triangle)

And thus, the total blue shaded area is 12√3 – 4π  (or approximately 8.22)

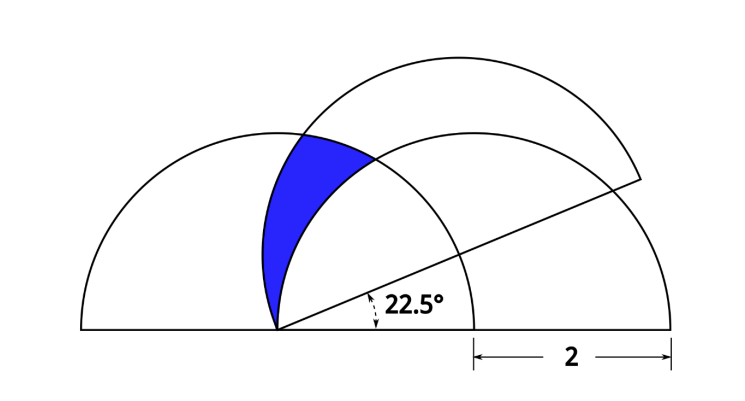
Fang Tango

Let’s color two more sections of the figure for clarity of the explanation.

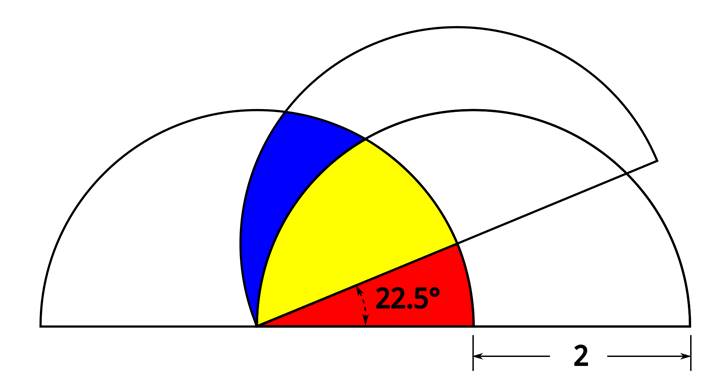
It can be seen that the areas of these two combined sections are identical (the only difference is rotation):

And if that is true then, we can subtract the area of the yellow section from both sides of the equation:

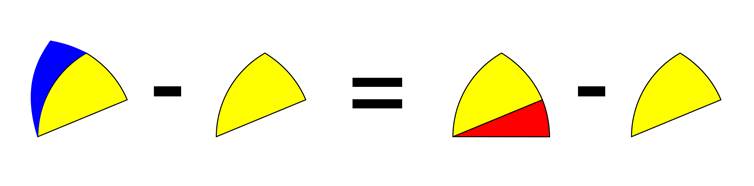
And that leaves the following equality:

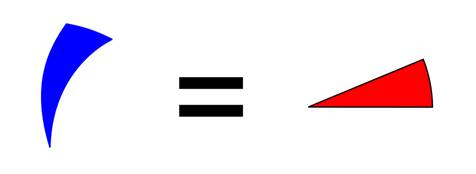
Thus, we know that the areas of the blue and red sections are identical.  The area of the red shaded section is somewhat easier to calculate:

It’s 22.5/360^ths or 1/16^th of the area of a 2” radius circle.  Or (π2²)/16 = π/4   (or approximately 0.79)