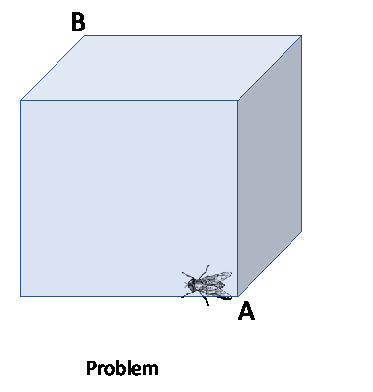
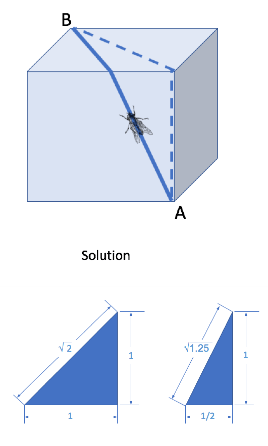
1.) The Fly’s Journey
The fly can crawl completely around the base of this solid cube in four minutes. How long would it take for it to crawl from corner A to corner B?
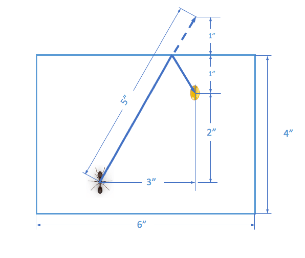
2.) The Ant and the Honey
An ant is on the outside of a cylinder one inch from the bottom. There is a drop of honey 180 degrees opposite the ant, but on the inside of the cylinder, and one inch from the top. If the cylinder is four inches tall and six inches in circumference, how far will the ant have to walk to reach the honey?

3.) The Squirrel’s Climb
A squirrel goes spirally up a cylindrical post, making one complete circuit in four feet (of post height). How many feet does the squirrel travel if the top of the post is sixteen feet high and three feet in circumference?

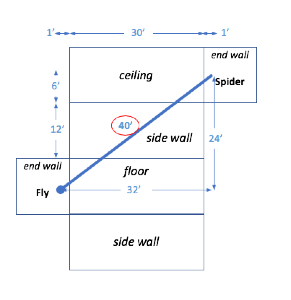
4.) The Spider and the Fly
There are a spider and a fly in a rectangular room 12 feet wide by 30 feet long, with a 12 foot ceiling. The spider is in the center of one end-wall, 1 foot from the ceiling, while the fly is in the center of the opposite end-wall, one foot from the floor. Assuming that the (oblivious) fly never moves – what is the shortest distance that the spider must crawl to catch his dinner?
Keep Scrolling for Answers
B
R
A
I
N
T
E
A
S
E
R
S
Brain Teaser Answers
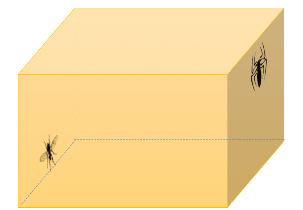
1.) The Fly’s Journey Solution
While the run-of-the-mill house fly might follow the path indicated by the dotted line below, it would need 2.41 minutes (1 + sq. root 2) to reach B. The clever fly would take the more direct (solid line) path, and reach B in 2.236 minutes (2 * sq. root 1.25)
2.) The Ant and the Honey Solution
It may help to “unroll” the cylinder as a mental exercise. And note that the “crossing over” of the upper edge of the cylinder can be “flipped” so that the entire path is represented by a straight line. The distance can then be calculated with a simple Pythagorean triangle. A right triangle with sides of 3” and 4” has a hypotenuse 5” in length. The ant would need to walk 5” to reach the honey.
3.) The Squirrel’s Climb
Similar to the previous puzzle – “unwrapping” the cylinder may help simplify the calculation. To make one revolution, the squirrel is climbing along the hypotenuse of a right triangle with sides of three feet and four feet in this case – for a total of 5 feet of travel per rev. To climb a pole sixteen feet tall, the squirrel must make four revolutions, and travel a total of twenty feet.
4.) The Spider and the Fly
There are a couple of answers to this one.
If the spider takes a direct path (parallel to the side walls), it would go up one foot, along the ceiling for 30 feet, and then 11 feet down the far wall, for a trip distance of 42 feet.

However, if the Spider is to crawl for the entire trip, the shortest path is shown here: