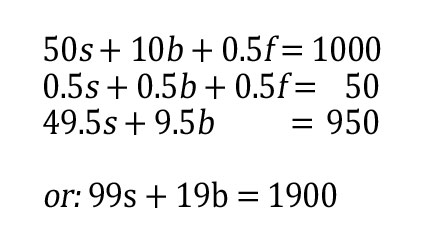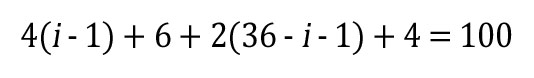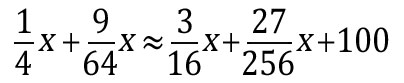In each issue of the Automation Notebook we feature a section of brainteasers. These are the brainteaser answers from Issue 20, 2011 of the Automation Notebook. The brainteaser questions are repeated in black. The answers to the brainteaser questions are highlighted in red with explanations. You can view the brainteasers from Issue 20, 2011 without the answers here: http://library.automationdirect.com/brainteasers-issue-20-2011/
1. Shopping Cart Jumble
An engineer went to: www.AutomationDirect.com to purchase some high-value automation parts. She purchased various quantities of three parts: proximity sensors at $50 each, Stable motor mounting bases at $10 each, and Nitra pneumatic fittings at $0.50 each. She purchased a total of 100 parts, and spent exactly $1000 dollars (qualifying her order for free 2-day shipping). Can you calculate how many of each part she purchased?
Answer: The Engineer bought 19 Proximity Sensors, 1 Stable™ Mounting Base and 80 Nitra™ Pneumatic Fittings.
Let s=number of sensors, b=number of bases, and f=number of fittings. We know that 50s+10b+0.5f=1000, and that s+b+f=100 (which can also be stated: 0.5s+0.5b+0.5f=50)
The only answer to this indeterminate equation is s=19, and b=1. And because we know that 100 total items were purchased, that leaves 80 fittings.
2. IO, IO, It’s off to Work We Go
A PLC system contains 36 I/O modules and a total of 100 I/O points. All the input modules are 4 point, and all the output modules are 2 point – except for one 6 point input and one 4 point output. Can you discern the number of input vs. output modules in the system?
Answer: There are 12 input modules and 24 outputs in the system
Let i = the number of input modules in the system, the total number of output modules will be 36-i
We can total the I/O points thusly:
Solve for i: i=12 input modules, and so the number of output modules must be 24
3. Quarter Time
The hopper of a packaging machine is filled with widgets on Monday morning. Each day the machine packages a single widget as a test sample, and then proceeds to package one quarter of the remaining widgets from the hopper. Recordkeeping is minimal, but it is noted that the number of widgets packaged on Monday and Wednesday is exactly 100 more than the number packaged on Tuesday and Thursday. At the end of the day, Thursday, the production manager asks how many widgets remain in the hopper. Can you tell him?
Answer: 321 Widgets remain in the hopper at the end of the day on Thursday.
Solving this problem out exactly using algebra quickly proves to be very complicated. But if we use some approximations, we can simplify things greatly. If we ignore the sample widget that is packed each day, we can state that approximately ¼ of the widgets were packaged on Monday, 3/16ths were packaged on Tuesday, 9/64ths on Wednesday and 27/256ths on Thursday.
So let x represent the total number of widgets at the beginning of the week. We know that Monday’s + Wednesday’s production equals Tuesday’s + Thursday’s production +100 widgets, so therefore:
Solving for x yields:
We know that the starting number of widgets must be an even multiple of 4, plus a single widget, and that this starting number is close to 1024. The closest such number is 1025, but it doesn’t work, because on Tuesday the machine would have to package a fraction of a widget. Stepping down to 1021 does work, with each day’s production as follows: Monday-256, Tuesday-192, Wednesday-144, Thursday-108, leaving 321 widgets in the hopper at the end of the day on Thursday.