Team Colors
Joe, Bob, Sue, and Robin are members of an FRC robotics team. Their team roles are, not necessarily respectively, President, Treasurer, Electrical Lead, and Mechanical Lead. They wear (again not-necessarily-respectively) red, blue, black and green shirts.
You are told that the President is better at math than Bob, and that Sue and the Electrical Lead often play video games with the team members in black and green shirts. Joe and the Mechanical Lead have lunch with the team member in the green shirt, but that isn’t the treasurer, as the treasurer always wears red.

What was the role and shirt color of each team member?
Are you aware of the FIRST Robotics Competition (FRC)? Learn more and get involved with a local team here. Read more about our involvement in THIS issue of Notebook.

Crossing the Line
A certain factory floor is tiled with identical square tiles, and is exactly 72 tiles wide x 90 tiles long. If a line is drawn from one corner of the factory to the opposite diagonal corner – how many of the tiles does that line cross?
What would the answer be if the floor measured 2982 x 3822 titles? Or, in other words – can you find the general solution to the problem for any size room?

Liar’s Club
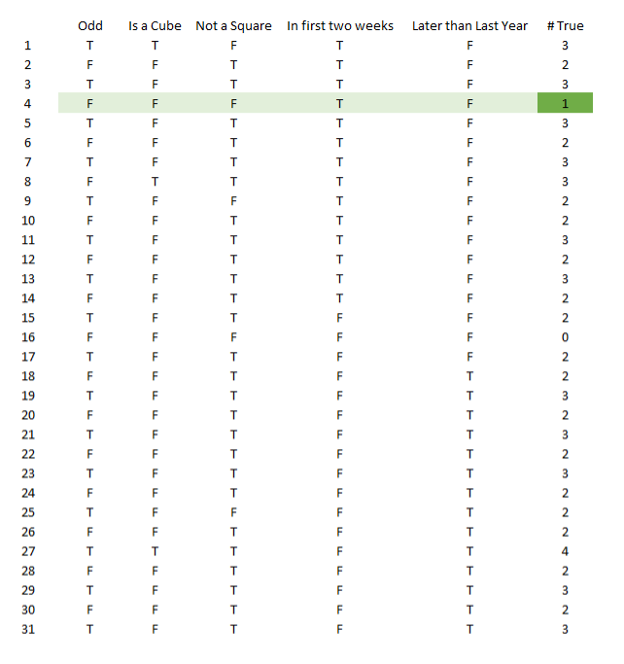
The annual Liars Club Dinner is (again) planned for May, but none of the members know which night the event will be held. That doesn’t stop some of the members from making the following claims at the March meeting: The first member stands to speak and claims that the date will be an odd number. A second member states that the date is a perfect cube, while the third member to speak reports that the date is not a perfect square. After the meeting, the president confides to the board that the meeting will be in the first week of the month. But the membership director (who is always having trouble collecting dues from deadbeat members) insists that the date must be later in the month than the date on which the event was held the previous year. That date is known to have been the 17th.
It was subsequently discovered that only one of the members was telling the truth. What is the date of the event?
All puzzles credit E. R. Emmet (1909-1980)
Answers Below!
–
–
–
–
–
–
–
–
–
–
Answers
Team Colors
From the setup of the puzzle we can rule out several colors and roles:
- President can’t be Bob
- Sue not the Electrical Lead
- Joe not Mechanical Lead
- Neither Sue nor Electrical Lead wears Black or Green
- Neither Joe nor Mechanical Lead wears Green
- The Treasurer wears Red, and therefore no other team role wears red
It may help to fill in a chart with that known information:
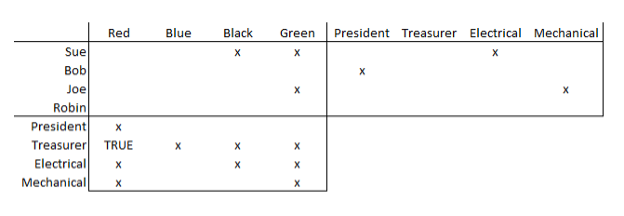
Then we can deduce (and continue filling in the chart):
We can fully complete the roles and colors (bottom left quadrant of the chart)
- The President must wear Green (as no one else wears Green), and also rule out blue and black for Pres…
- Therefore the Mechanical Lead must wear Black, and rule out blue for Elec
- Therefore the Electrical Lead must wear Blue
Then, because we know:
- Bob is not the president…
- The President wears green…
- Yet Sue and Joe don’t wear Green…
THEN therefore Robin must be the President
Now:
- We know Sue doesn’t wear black…
- But that the Mechanical Lead DOES wear Black…
- And that Joe nor Robin is the Mechanical Lead…
Therefore Bob must be the Mechanical Lead
That leaves the only possible role for Sue to be the Treasurer
And therefore Joe must be the Electrical Lead
So the roles and colors are:
Sue: Red: Treasurer
Bob: Black: Mechanical Lead
Joe: Blue: Electrical Lead
Robin: Green: President
Crossing the Lines
A picture may help:
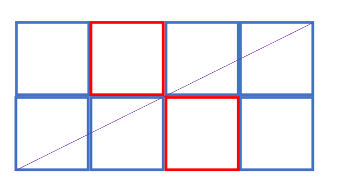
In this simple case we can see that the line crosses four of the tiles on a 2 x 4 grid.
The line crosses all four(4) columns of tiles from right to left – once and only once – and both(2) of the rows of tiles from top to bottom – once and only once. But note that in the center of the grid – the line goes directly through the intersection of four tiles and only crosses the blue tiles.
So if we know how many “exact intersection” crossings there are, then the general formula will be pretty easy to determine:
- Total tiles crossed = number of rows + number of columns – the number of exact intersections
So, the trick becomes how to calculate the intersections. This number is the Greatest Common Factor(GCF) of the two numbers (width and length).
The greatest common factor of 2 and 4 is 2.
So, for our simple example above with 4 tiles wide x 2 tiles long – the number of tiles crossed is = 2 + 4 – 2 = 4 tiles.
The greatest common factor of 72 and 90 is 18.
So, with 72 tiles wide x 90 tiles long – the number of tiles crossed in the original problem statement is = 72 + 90 – 18 = 144 tiles.
And the extra credit: the CFG of 2982 and 3822 is 42, so the number of tiles crosses is 2982 + 3822 – 42 = 6762 tiles.
Liar’s Club
It may help to make a chart. We are looking for the only row with a single true statement. The dinner was held on the 4th.