I think we’ve all been confronted with a challenging application at one time or another. In this particular instance, I was contacted by a customer asking for help with an application using a floating-point number that needed four decimal places. Even though the fourth decimal place was not being used, it had to have a value in it in order to make an ASCII string work properly to a remote device. The other part of the challenge was that the ASCII string would not work if there were more than four decimal places. The customer did not want to have to go through the stored ASCII to find the decimal point and to determine if there were more or less than four digits after it.
The Challenge
My challenge was to find an easy way to check whether or not a value was in the fourth position, add one if needed, and drop any decimal places greater than four. I was able to accomplish this in three rungs of logic using a CPU that using real math and bit-of-word programming instructions.
The first step was to take the real number with decimal places and make it a whole number by multiplying by a factor of 10,000 (real). Once I had a whole number, I converted it to a binary number to discard any extra decimal places. Then I converted it to a 32-bit binary coded decimal number (BCD). The purpose of using a BCD number is that I could look at the least significant nibble (LSN) of the word. The LSN represents the fourth digit in my decimal number.
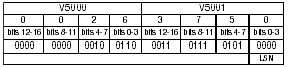
Using the real number 26.37501, the conversion to BCD bit pattern would look as follows:
32-bit word (two 16-bit words V5000 & V5001)
Remember, I only multiplied by 10,000, therefore the fifth decimal place (1) was not converted to BCD.
The next step was to look at the status of the four bits that make up the LSN (bits 0-3). If the status of each bit was null (off), I needed to add a value of .0001 to the real number.
The last step was to make sure there were no more than four decimal places in the number. So by multiplying by 10,000 (real), converting to a binary number (no decimal places), and then back to a real number, there would be four decimal places.
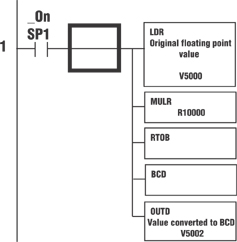
Now the real number will be 26.3751. The ladder would be as follows:
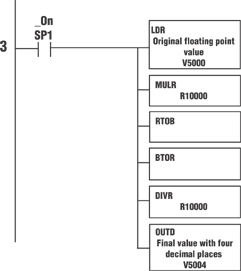
Rung 1 takes the Real value in V5000, multiplies it by 10,000 to move the decimal point over four places. It then converts it to Binary to cut off any left over decimal places. The number is then converted to BCD and stored in V5002.
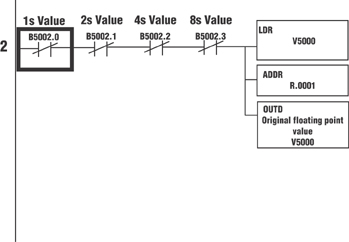
Rung 2 checks the first nibble, bits 0-3 of the BCD number in V5002, to see if any of the bits are on. If all of them are off, the fourth digit of the decimal value is a zero, so a value of .0001 must be added.
To guarantee a four decimal point value, the number is multiplied by 10,000 then converted to a Binary number to drop any decimal places. It is then converted back to a Real number, divided by 10,000, giving it only four decimal places. The result is stored in V5004.
by Doug Bell,
Interconnecting Automation
www.interconnectingautomation.com
Originally Published: April 1, 2004