There are several types of numbering systems typically used in automation equipment: Binary, Hexadecimal, Octal, BCD and Floating Point (Real). How to use them can be confusing. This article, from our Technical Support web page, explains the different numbering systems.
Binary Numbers
Computers, including PLCs, use the Base 2 numbering system called Binary or Boolean. There are only two valid digits in Base 2: 0 and 1 (OFF and ON). You would think it would be hard to have a numbering system built on Base 2 with only two possible values, but it can be done by encoding, using several digits.
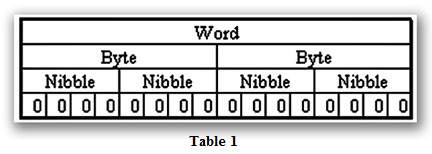
Each digit in the Base 2 system, when referenced by a computer, is called a bit. When four bits are grouped together, they form what is known as a nibble. Eight bits—or two nibbles—is a byte. Sixteen bits – or two bytes – is a word (Table 1). Thirty-two bits—or two words—is a double-word.
Binary is not “natural” for us since we grew up using the base 10 system, which uses numbers 0-9. In this article, the different bases will be shown as a subscripted number. For example, 10 decimal would be 1010.
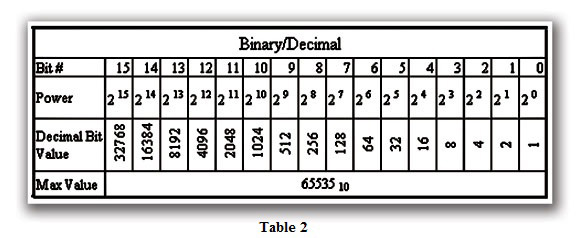
Table 2 shows how Base 2 numbers relate to their decimal equivalents.
A nibble of 10012 would be equal to a decimal number 9 or (1*23 + 1*20) or (810 + 110). A byte of 110101012 would be equal to 21310 or (1*27 + 1*26 + 1*24 + 1*22 + 1*20) or (12810 + 6410 + 1610 + 410 +110).
Hexadecimal Numbers
As you have probably noticed, the Binary numbering system is not very easy to interpret. For a few bits, it is easy, but larger numbers tend to take up a lot of room when writing them down and it is difficult to keep track of the bit position while doing the conversion. That is where using an alternate numbering system can be an advantage. One of the first numbering systems used was Hexadecimal, or Hex for short.
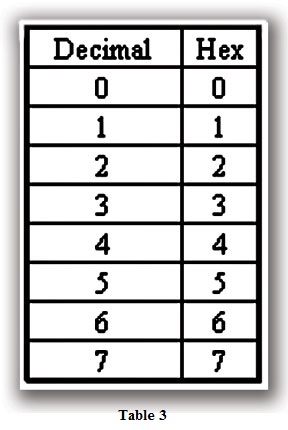
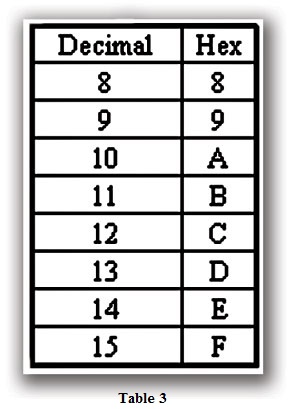
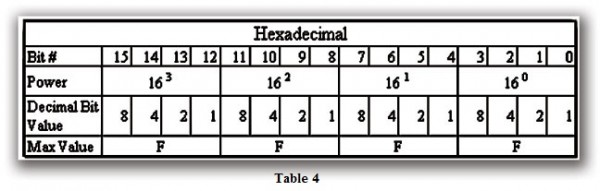
Hex is a numbering system that uses Base 16. The numbers 0-910 are represented normally, but the numbers 1010 through 1510 are represented by the letters A through F, respectively (Table 3). This works well with the Binary system as each nibble (11112) is equal to 1510. Therefore, for a 16-bit word, you could have a possible Hex value of FFFF16. See Table 4 for an example.
Hex-to-decimal conversions work in much the same way as Binary. C216 would be equal to 19410 or (12*161 + 2*160) or (19210 +210). A6D416 would be equal to 4270810 or (10*163 +6*162 +13*161 +4*160) or (4096010 + 153610 + 20810 +410).
Octal Numbers
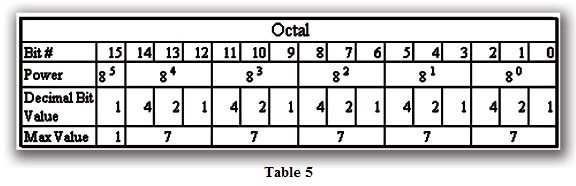
The Octal numbering system is similar to the Hexadecimal system in the interpretation of the bits (Table 5). The difference is the maximum value for Octal is 7, since it is a Base 8.
For example, 638 is equal to 5110 or (6*81 + 3*80) or (4810 +310).
BCD Numbers
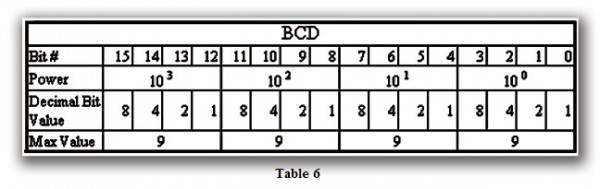
The BCD numbering system, like Octal and Hexadecimal, relies on bit-coded data (Table 6). It is Base 10 (Decimal), but it is Binary Coded Decimal. There is a big difference between BCD and Binary, as we will see later.
One plus of BCD coding is that it reads like a Decimal number, whereas 867 BCD would mean 867 Decimal. No conversion is needed. However, as with all things computer related, there are snags to worry about.
Real (Floating Point) Numbers
The terms Real and Floating Point both describe IEEE-754 floating point numbers. Most PLCs use a 32-bit format for floating point (real) numbers (Table 7).
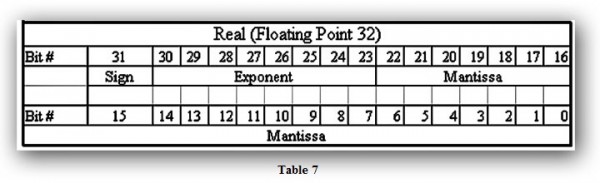
The formula and layout of the number is as follows:
Number = 1.M*2(E-127)
Number = the number to be converted to floating point
M = Mantissa
E = Exponent
Calculating the Real number format is a very complex operation. If you are interested in the conversion process, there are numerous documents on the Internet that go into specific detail.
You may have noticed that there is not a minimum or maximum value given for the Real number format. The range is from negative infinity to positive infinity. Having said this, and having noticed that there are only 32 bits possible to create every number, it is easy to surmise that not all numbers can be represented. This is in fact the case. There is an inherent extent of error with the Real format.
I’m sure you’re wondering how much error can exist and if there is a lot of error, why is this format used? It really depends on the application. For most PLC applications, unless you are aiming for 100% accuracy, the Real format will not pose many problems. Most of the time the inherent error can be ignored, but it is important to know it exists.
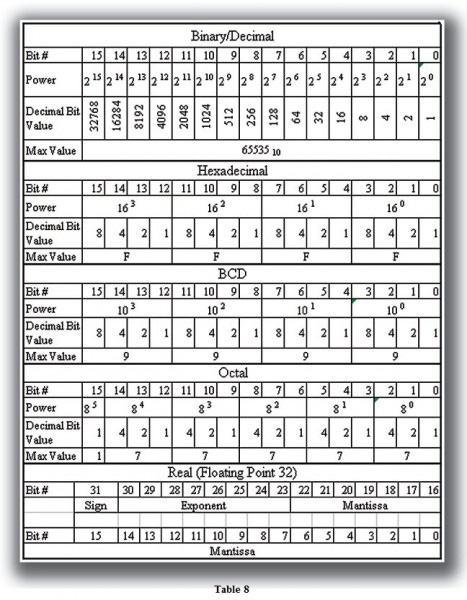
BDC/Binary/Decimal/Hex/Octal – What is the Difference?
Sometimes there is confusion about the differences between the data types used in a PLC. Although data is stored in the same manner (0’s and 1’s), there are differences in the way that a PLC interprets it.
While all of the formats rely on the Base 2 numbering system and bit-coded data, the format of the data is dissimilar. Table 8 shows the bit patterns and values for the various formats.
Data Type Mismatch
Data type mismatching is a common problem when using an operator interface. Diagnosing it can be a challenge until you identify the symptoms. Since a PLC uses BCD as the native format, many people tend to think it is interchangeable with Binary (unsigned integer) format. This is true to some extent, but not in this case. Table 9 shows how BCD and Binary numbers differ.
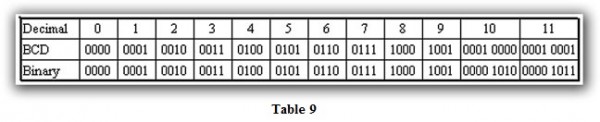
As the table shows, BCD and Binary share the same bit pattern until you get to the decimal number 10. Once you get past 10, the bit pattern changes. The BCD bit pattern for the decimal 10 is actually equal to a value of 16 in Binary, causing the number to jump by six digits when viewing as BCD. With larger numbers, the error multiplies. Binary values from 10 to 15 Decimal are actually invalid for the BCD data type.
Let’s look at a larger number shown in Table 10.
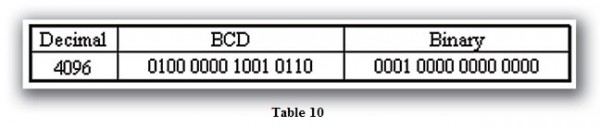
As a BCD number, the value is 4096. If we interpret the converted BCD number as Binary, the Decimal value would be 16534. Similarly, if we interpret the Binary number as BCD, the Decimal value would be 1000.
Signed vs. Unsigned Integers
So far, we have dealt with unsigned data types only. Now let’s talk about signed data types (negative numbers). BCD representation cannot be used for signed data types.
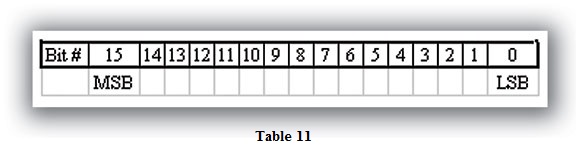
In order to signify that a number is negative or positive, we must assign a bit to it. Usually, this is the Most Significant Bit (MSB) as shown in Table 11. For a 16-bit number, this is bit 15. This means that for 16-bit numbers we have a range of -32,767 to 32,767.
We have two ways of encoding a negative number: Two’s Complement and Magnitude Plus Sign. The two methods are not compatible.
As long as the value is positive (bit 15 is OFF), then the rules work similarly to binary. If bit 15 is ON, then we must know which encoding method was used.
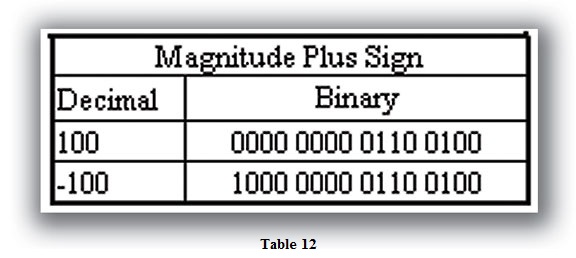
The Magnitude Plus Sign is the easiest to decode. Basically, the negative number is in the same format as the positive number, except with bit 15 ON (Table 12).
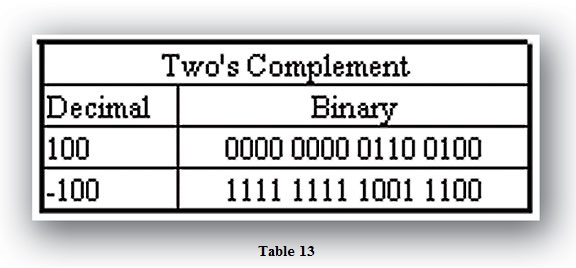
Two’s Complement is slightly more difficult. The formula is to invert the binary value and add one (Table 13).
Obviously, numbering systems vary and yet are similar. It is vital to know which system is being used in order to program the application properly. A methodical and logical approach to understanding a given number system being used makes interpreting the data less complex.
Originally Published: Sept. 1, 2005 / Reviewed Jan 22, 2021